Álgebra Superior.
Números
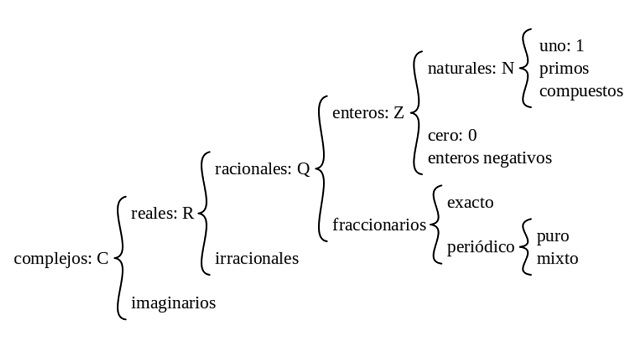
Para empezar vi que son los números, y cómo se clasifican para ello tuve que ver videos relacionado sobre ello y uno que me despejo de dudas fue este: https://www.youtube.com/watch?v=rtNC7g1h_JAEn el cual nos habla sobre cómo se clasifican los números diciendo que empiezan por los complementarios ya que todo número tiene 1 número real y 1 imaginario pero a veces 1 sin el otro y ahí es donde se deriva a los reales que son el conjunto de los números reales incluyen tanto a los números racionales como a los número racionales y de ahí los racionales son todos los números que pueden representarse como el cociente de dos números enteros o, más exactamente un entero y un natural positivo., de ahí pasa a los irracionales que es un número que no puede ser expresado como una fracción ᵐ⁄ₙ, donde m y n son enteros y n sea diferente de cero. Es cualquier número real que no es racional, y su expresión decimal no es ni exacta ni periódica
El segundo tema es sobre desigualdades el cual tuve que ver este vídeo youtube.com/watch?v=jSZWvCh2PqI el cual es sobre un ejercicio bien explicado sobre como resolver una desigualdad con un buen método de las rectas, el cual yo utilice durante las practicas.
En el tercer tema vimos sobre vectores el primero fue multiplicación producto punto https://www.youtube.com/watch?v=gRPzgx75_uo el cual es lo mas fácil porque multiplicas variables correspondientes y después puedes sacar mas cosas de vectores
En el cuarto tema vimos proyecciones https://www.youtube.com/watch?v=d4_6-kF1HdY el cual nos da formulas para poder hallarlos de igual manera nos explica que es y para que sirve, el cual es el "retoño" de un vector y por lo tanto se denomina vector unitario que es 1 y después con la formula se puede sacar la proyección con respecto a otro vector, este video me ayudo mucho ya que me confudia mucho utilizando las formulas y me aclaro todas mis dudas.
hemos estado viendo matrices...si, estresante, pero no tan complicado como parece, y es que a pesar de todo, existen distintos metodos para resolver este tipo de ejercicios; uno de estos es el método de Gauss-Jordan, una breve explicación de su algoritmo según wikipedia:
Si la primera fila tiene un cero en esta columna, intercambiarlo con otra que no lo tenga.
Luego, obtener ceros debajo de este elemento delantero, sumando múltiplos adecuados del renglón superior a los renglones debajo de él.
Cubrir el renglón superior y repetir el proceso anterior con la submatriz restante. Repetir con el resto de los renglones (en este punto la matriz se encuentra en forma escalonada).
Comenzando con el último renglón no cero, avanzar hacia arriba: para cada renglón obtener 1 delantero e introducir ceros arriba de éste sumando múltiplos correspondientes a los renglones correspondientes.
Una variante interesante de la eliminación de Gauss es la que llamamos eliminación de Gauss-Jordan, (debido al mencionado Gauss y a Wilhelm Jordan), esta consiste en ir obteniendo los 1 delanteros durante los pasos uno al cuatro (llamados paso directo) así para cuando estos finalicen ya se obtendrá la matriz en forma escalonada reducida.
Un pequeño ejemplo sería el siguiente:
Paso un dia y el maestro nos dijo que teniamos que exponer de cualquier tema que hayamos visto en el semestre entonces me reuni con mi equipo y decidimos el tema, pero para ellos vimos cual nos convenia mas y lo decidimos con este video https://www.youtube.com/watch?v=MuCEb3M-HjQ y este causlamente el ultimo que vimos en el semestre entonces nuesta mente estaba fresca con el tema y se nos facilitó aun más.
Y con esto concluimos el semestre.
Desigualdades
El segundo tema es sobre desigualdades el cual tuve que ver este vídeo youtube.com/watch?v=jSZWvCh2PqI el cual es sobre un ejercicio bien explicado sobre como resolver una desigualdad con un buen método de las rectas, el cual yo utilice durante las practicas.
Vectores
En el tercer tema vimos sobre vectores el primero fue multiplicación producto punto https://www.youtube.com/watch?v=gRPzgx75_uo el cual es lo mas fácil porque multiplicas variables correspondientes y después puedes sacar mas cosas de vectores
Proyecciones
En el cuarto tema vimos proyecciones https://www.youtube.com/watch?v=d4_6-kF1HdY el cual nos da formulas para poder hallarlos de igual manera nos explica que es y para que sirve, el cual es el "retoño" de un vector y por lo tanto se denomina vector unitario que es 1 y después con la formula se puede sacar la proyección con respecto a otro vector, este video me ayudo mucho ya que me confudia mucho utilizando las formulas y me aclaro todas mis dudas.
Matrices
En el quinto tema vimos matrices que esto ya es de la segunda secuencia el maestro nos explico todo sobre matrices y como sumarlas, restarlas, multiplicar y dividir. Nos enseñó varios ejemplos y todo quedó entendido en la clase pasando essto a la siguiente clase nos puso unos ejercicios y regaló puntos extras pero mando ejercicios mas complicados y necesite la ayuda de Yotube y busque este video en especifico porque un amigo me lo pasó: https://www.youtube.com/watch?v=ajvwN6FogKI despues de haber visto este video resolvió todas mis dudas pudiendo realizar mi exmanen de este tema, pasamos a otro metodo y la verdad estuvo facil para mi ya que lei y observé por ahí un video lo cual lo pongo: https://www.youtube.com/watch?v=ZO0naBrmgj4. Pasamos a otra muy particular que era resolver matrices mediante la aplicación Matlab y me eche unos ejercicios para poner en practica y para ello ocupé este video: https://www.youtube.com/watch?v=Ll5kqRiq90Q con el cual pudre realizar otra evaluación concluyendo el segundo parcial.hemos estado viendo matrices...si, estresante, pero no tan complicado como parece, y es que a pesar de todo, existen distintos metodos para resolver este tipo de ejercicios; uno de estos es el método de Gauss-Jordan, una breve explicación de su algoritmo según wikipedia:
Si la primera fila tiene un cero en esta columna, intercambiarlo con otra que no lo tenga.
Luego, obtener ceros debajo de este elemento delantero, sumando múltiplos adecuados del renglón superior a los renglones debajo de él.
Cubrir el renglón superior y repetir el proceso anterior con la submatriz restante. Repetir con el resto de los renglones (en este punto la matriz se encuentra en forma escalonada).
Comenzando con el último renglón no cero, avanzar hacia arriba: para cada renglón obtener 1 delantero e introducir ceros arriba de éste sumando múltiplos correspondientes a los renglones correspondientes.
Una variante interesante de la eliminación de Gauss es la que llamamos eliminación de Gauss-Jordan, (debido al mencionado Gauss y a Wilhelm Jordan), esta consiste en ir obteniendo los 1 delanteros durante los pasos uno al cuatro (llamados paso directo) así para cuando estos finalicen ya se obtendrá la matriz en forma escalonada reducida.
Un pequeño ejemplo sería el siguiente:
Números imaginarios
Nuestra ultima asignación de álgebra ha sido acerca de los números complejos, para ser mas precisos, números imaginarios. Todo lo que tiene que ver con estos: desde multiplicación, división, suma y resta, hasta ver incluso dos métodos para la división y la multiplicación, ademas de las distintas formas de representarlos.
La unidad imaginaria
La columna vertebral de este nuevo sistema de números es la unidad imaginaria, o sea el número iii.
Las siguientes propiedades son verdaderas para el número iii:
i=\sqrt{-1}i=
−1
i, equals, square root of, minus, 1, end square root
i^2=-1i
2
=−1i, squared, equals, minus, 1
La segunda propiedad demuestra que el número iii sí es una solución de la ecuación x^2=-1x
2
=−1x, squared, equals, minus, 1. La ecuación que previamente era insoluble, ¡ahora tiene una solución, al agregar la unidad imaginaria!
Números imaginarios puros
El número iii ¡de ninguna manera está sólo! Al utilizar múltiplos de esta unidad imaginaria, podemos crear una infinidad de otros números imaginarios puros.
A saber, 3i3i3, i, i\sqrt{5}i
5
i, square root of, 5, end square root, y -12i−12iminus, 12, i, son ejemplos de números imaginarios puros; o sea, números de la forma bibib, i, donde bbb es un número real diferente de cero.
Elevar estos números al cuadrado ilustra cómo se relacionan con los números reales. Investiguemos esto al elevar el número 3i3i3, i al cuadrado. Las propiedades de exponentes enteros son las mismas, así que podemos elevar 3i3i3, i al cuadrado tal como podemos imaginarlo.
\begin{aligned}(3i)^2&=3^2i^2\\ \\ &=9{i^2}\\\\ \end{aligned}
(3i)
2
=3
2
i
2
=9i
2
Por el hecho de que i^2=-1i
2
=−1i, squared, equals, minus, 1, podemos simplificar esto aún más como sigue.
\begin{aligned}\phantom{(3i)^2} &=9\goldD{i^2}\\\\ &=9(\goldD{-1})\\\\ &=-9 \end{aligned}
(3i)
2
=9i
2
=9(−1)
=−9
El hecho que (3i)^2=-9(3i)
2
=−9left parenthesis, 3, i, right parenthesis, squared, equals, minus, 9 significa que 3i3i3, i es una raíz cuadrada de -9−9minus, 9.
Fuente: https://es.khanacademy.org/math/algebra2/introduction-to-complex-numbers-algebra-2/the-imaginary-numbers-algebra-2/a/intro-to-the-imaginary-numbers
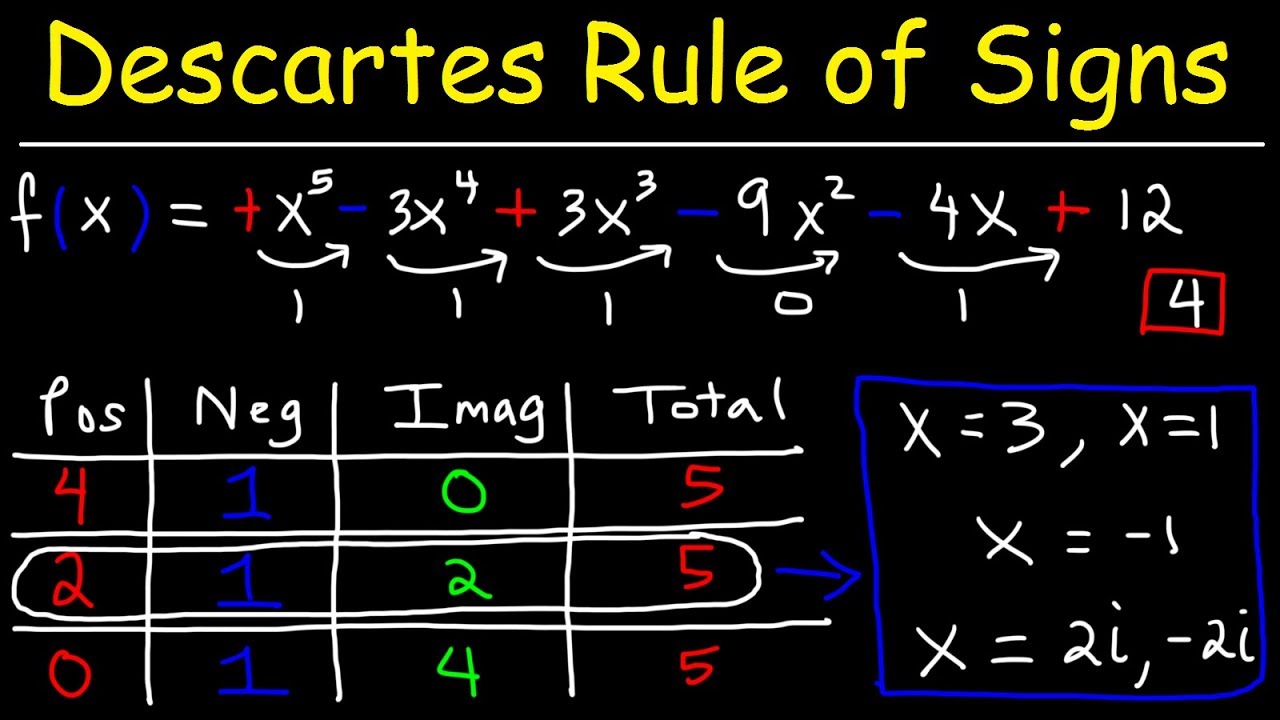
Ley de Descartes
En el tercer parcial solo fue un tema que teniamos que tener conocimentos previos para poder realizar los ejecicios (los conocimientos previos eran de la materia Matematicas Basicas), pero el tema en concreto era La ley de Descarte's el cual nos explico el maestro pero despues de la clase tuve mis dudas sobre como hacerlo con mas variables y mire este video: https://www.youtube.com/watch?v=6lI8Z_A4DRM.Paso un dia y el maestro nos dijo que teniamos que exponer de cualquier tema que hayamos visto en el semestre entonces me reuni con mi equipo y decidimos el tema, pero para ellos vimos cual nos convenia mas y lo decidimos con este video https://www.youtube.com/watch?v=MuCEb3M-HjQ y este causlamente el ultimo que vimos en el semestre entonces nuesta mente estaba fresca con el tema y se nos facilitó aun más.
Y con esto concluimos el semestre.




Excelente, me ayudas para mi examen
ResponderEliminarEste comentario ha sido eliminado por el autor.
ResponderEliminarCumple tus metas
ResponderEliminarSuerte !!!!!
Échale ganas
ResponderEliminar